| University | National University of Singapore (NUS) |
| Subject | Computational Fluid Dynamics |
MA4814 Computational Fluid Dynamics Assignment, NUS, Singapore Apply the finite volume technique to discretize and solve one-dimensional fully developed laminar
• Learning Objectives
- Determine the criterion for grid convergence for a laminar one-dimensional channel flow
- Solve nonlinear one-dimensional channel flow for non-Newtonian fluid
Problem 1
Apply the finite volume technique to discretize and solve one-dimensional fully developed laminar flow between two horizontal parallel plates governed by
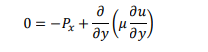
𝑢𝑢 is the velocity, 𝑃𝑃𝑥𝑥 is the pressure gradient and µ is the viscosity. In conservative form, this can be written as
![]()
Hire a Professional Essay & Assignment Writer for completing your Academic Assessments
In your solution show:
• A sketch for the cells, clearly marking faces and nodes for internal and boundary cells.
• Apply the linear approximation and use Dirichlet (velocity specified) boundary conditions to determine the approximate equations for internal and boundary cells.
• Compute the velocity distribution and compare your result with the exact solution, by adapting one of the uploaded codes. The number of grid cells is left up to you to determine. The solution must be grid converged.
For the numerical solution, let 𝑃𝑃𝑥𝑥 = 2µ, ℎ = 0.1, 𝑢𝑢(0) = 𝑢𝑢1 = 0.01, & 𝑢𝑢(ℎ) = 𝑢𝑢2 = 0. For grid convergence, you may define an error norm , and require that the error is less than 0.01𝑢 = 0.01 × 0.01. The exact solution is given by
![]()
Problem 2
Apply the finite volume technique to discretize and solve one-dimensional fully developed laminar non-Newtonian flow between two horizontal parallel plates governed by,
![]()
𝑢𝑢 is the velocity, 𝑃𝑃𝑥𝑥 is the pressure gradient. For non-Newtonian fluids, the viscosity µ𝑒𝑒 depends on the flow strain rate, which for one-dimensional fully developed flow is approximated by,
![]()
where 𝜇𝜇𝑜𝑜, 𝜅𝜅 are constants. Non-Newtonian fluids exist in several important applications, particularly in fluids using in printing, molten plastics used in 3D printers and most important for us, in blood and rheological flows. For more insight, you can check https://www.rheosense.com/applications/viscosity/newtonian-non-newtonian to learn more about
the shear thinning and thickening effects. As this is a non-linear problem, it is highly recommended
you follow the suggested algorithm:
Buy Custom Answer of This Assessment & Raise Your Grades
Empower your academic journey with our specialized services crafted for Singaporean students! At [Your Company Name], we excel in providing top-notch assignment help Singapore students trust. Whether you're navigating intricate subjects like Computational Fluid Dynamics at the National University of Singapore (NUS) or seeking assistance with Essay Writing Services and final year exam assignments, our expert team is at your service. When it comes to the MA4814 Computational Fluid Dynamics Assignment at NUS, we're here to help you apply the finite volume technique for one-dimensional fully developed laminar flow. Don't let academic challenges hold you back; trust our experts to ensure your success. Connect with us today and conquer your academic goals!
- Imagine that you are currently working for a precision medicine startup: Machine Learning Paper Review in Precision Medicine, Written Assignment 1, NUS, Singapore
- Go Business offers PSG solutions for enterprises in Singapore: Collective Intelligence and Entrepreneurship, Assignment 1, JCU, Singapore
- Design an ontology based on- Accidents can be categorised as chemical, electrical, fire, kinetic or liquid: Collective Intelligence and Entrepreneurship, Assignment 1, JCU, Singapore
- Project Control Monitoring, Assignment, HU, Singapore: Deliberate Project MONITORING AND CONTROL or PMC Identification
- DSM500: Final Project Report, Coursework 2, UOL, Singapore
- DSM080: Financial Markets, Assignment, UOL, Singapore: A grapefruit juice futures contract is for 15,000 pounds of frozen grapefruit juice
- DSM080: Financial Markets, Assignment, UOL, Singapore: The share price of a certain stock today is $42.50, and five-month European style call options with a strike price of $45 currently sell for $4.25.
- DSM080: Financial Markets, Assignment, UOL, Singapore: A trader who is working in the gold markets is able to borrow money at the interest rate of 7% per annum
- DSM080 Financial Markets, Assignment, UOL, Singapore: A dollar-based American corporation has decided that it will have to pay 6 million UK pounds in three months
- Principle of Finance Assignment, UCD, Singapore: National Gaming Inc. (National) operates the weekly lottery in the country
UP TO 15 % DISCOUNT

