MTH316 Assignement 01: Multivariable Calculus -Singapore University of Social Sciences (SUSS)
| University | Singapore University of Social Science (SUSS) |
| Subject | MTH316 Multivariable Calculus |
TUTOR-MARKED ASSIGNMENT 01 (TMA01)
This assignment is worth 12% of the final mark for MTH316 Multivariable Calculus.
The cut-off date for this assignment is 27 February 2025, 2355hrs.
Note to Students:
You are to include the following particulars in your submission: Course Code, Title of the
TMA, SUSS PI No., Your Name, and Submission Date.
For example, ABC123_TMA01_Sally001_TanMeiMeiSally (omit D/O, S/O). Use underscore
and not space.
Question 1
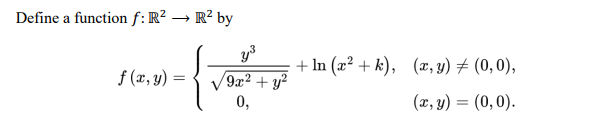
(a) Determine the value of k for the function 𝑓 to be continuous at (0, 0), if any. (Use this value of k for the following sub-questions.) (10 marks)
(b) Show that 𝑓𝑥 (0, 0) and 𝑓𝑦 (0, 0) both exist and find their values. (10 marks)
(c) Define 𝑓𝑥 (𝑥, 𝑦) and 𝑓𝑦 (𝑥, 𝑦) each as a piecewise function in the entire domain of ℝ2. (12 marks)
(d) Hence or otherwise, explain whether the function 𝑓 is differentiable at (0,0).
(18 marks)
Question 2
A GPS application designed for hikers measures the altitude, z, at various positions on a terrain and performs a regression, yielding the altitude function below, where x, y and z are measured in km.
![]()
(a) State an equation that describes the level set of the function and use it to plot the contours of the terrain at the altitudes of 1.3 km, 1.5 km and 2 km with a graph plotter. Attach a screenshot of the graph and label each contour with its equation clearly. (8 marks)
(b) A hiker crosses the position (0, 1) while walking along a contour. Determine the contour equation and calculate the gradient vector of the terrain function at the position (0, 1). Show that this gradient vector is orthogonal to the contour at the position (0, 1). (18 marks)
(c) A hiker is walking along a path given by 𝑦 = 1 − 𝑥 − 𝑥 3 . Sketch the path on your graph in part (a) and compute the directional derivative along the path at (0, 1) in the direction of increasing altitude. Explain briefly the meaning of this value of the directional derivative. (10 marks)
(d) The GPS carried by the hiker in part (c) shows that his ground speed is 0.8 m/s. Compute the rate of ascent (with respect to time) of the hiker as he crosses (0, 1). What is the degree of slope and how fast is he walking in the upslope direction? (7 marks)
(e) Another hiker is planning to walk from (5/2, 5/4) to (4, 2) in a straight line. From the contours plotted in part (a), explain the terrain he will experience along this path (without using calculations). (7 marks)
Hire a Professional Essay & Assignment Writer for completing your Academic Assessments
- 7005MHR Leadership: Towards Mastery of Leading Change and Inclusivity Assignment
- PSB7005CL Leadership: Towards Mastery of Leading Change and Inclusivity Assignment Brief
- BBS67 Principle of Finance Individual Assignment Question | UoM
- HS3225 Transition and Palliative Care Written Assignment | Nanyang Polytechnic
- NUR 3015 Health and Social Policy Summative Assignment Report 2025/26 | SIT
- PS5009MKT Digital Business Assessment Coursework | Coventry University
- 5007MKT Marketing Insight Assignment Coursework 2 – Coffee Shop Industry
- HL3044 The Legends of King Arthur Assignment Semester 1, AY2025-26 | NTU
- AVM343 Airport Design and Planning End-of-Course Assessment – July Semester 2025
- BX2091 Tourism & Leisure Management Assessment 3 Research Workbook 2026 | JCU


